아래와 같은 지수함수를 미분을 해봅시다.
증명을 할려면 도함수의 정의식에 넣고 길게 전개를 해야하나 오늘은 간단하게 한번 해볼 예정.
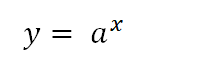
첫번째 단계는 위 식을 아래와 같이 변형을 시켜놓자. e의 ln승은 소거되어 없어지기 때문에 결국엔 같은식이다.

맨 마지막에 있는 x승을 ln앞으로 내리자.

자 이제 위의 식을 가지고 미분에 들어간다.
위 식은 e의 x승 꼴인데 합성함수이다.
그럼 합성함수 미분하듯이 해보자.
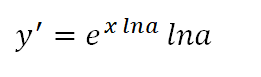
지수쪽에 있는 x lna를 x로 미분하면 lna가 된다. 이 lna를 곱해준다.
e의 x승을 미분하면 그대로 e의 x승이므로 위와 같은 식이 된다.
그럼 다시 x lna에서 x를 위로 올리면 아래와 같다.
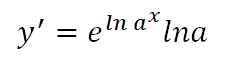
위의 식에서 자연로그를 없애주면 짜잔~ 아래와 같다.
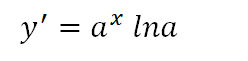
간단히 유도가 되므로 따로 공식으로 외우지 않아도 될거 같다.
'AI > Math' 카테고리의 다른 글
| [미적분]미분공식 (0) | 2019.09.24 |
|---|---|
| [미적분]y=x^n 미분하기 (0) | 2019.09.24 |
| [미적분]몫의 미분법 (0) | 2019.09.24 |
| [미적분]삼각함수 sin x / x 의 극한 그래프 (0) | 2019.09.23 |
| [미적분]Limit 너란 녀석 (0) | 2019.09.23 |