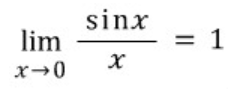
보통 위의 극한식을 증명하기 위해 샌드위치 정리를 이용하여 증명을 한다.
오늘은 그래프로 어떤 느낌인지 알아볼 예정이다.
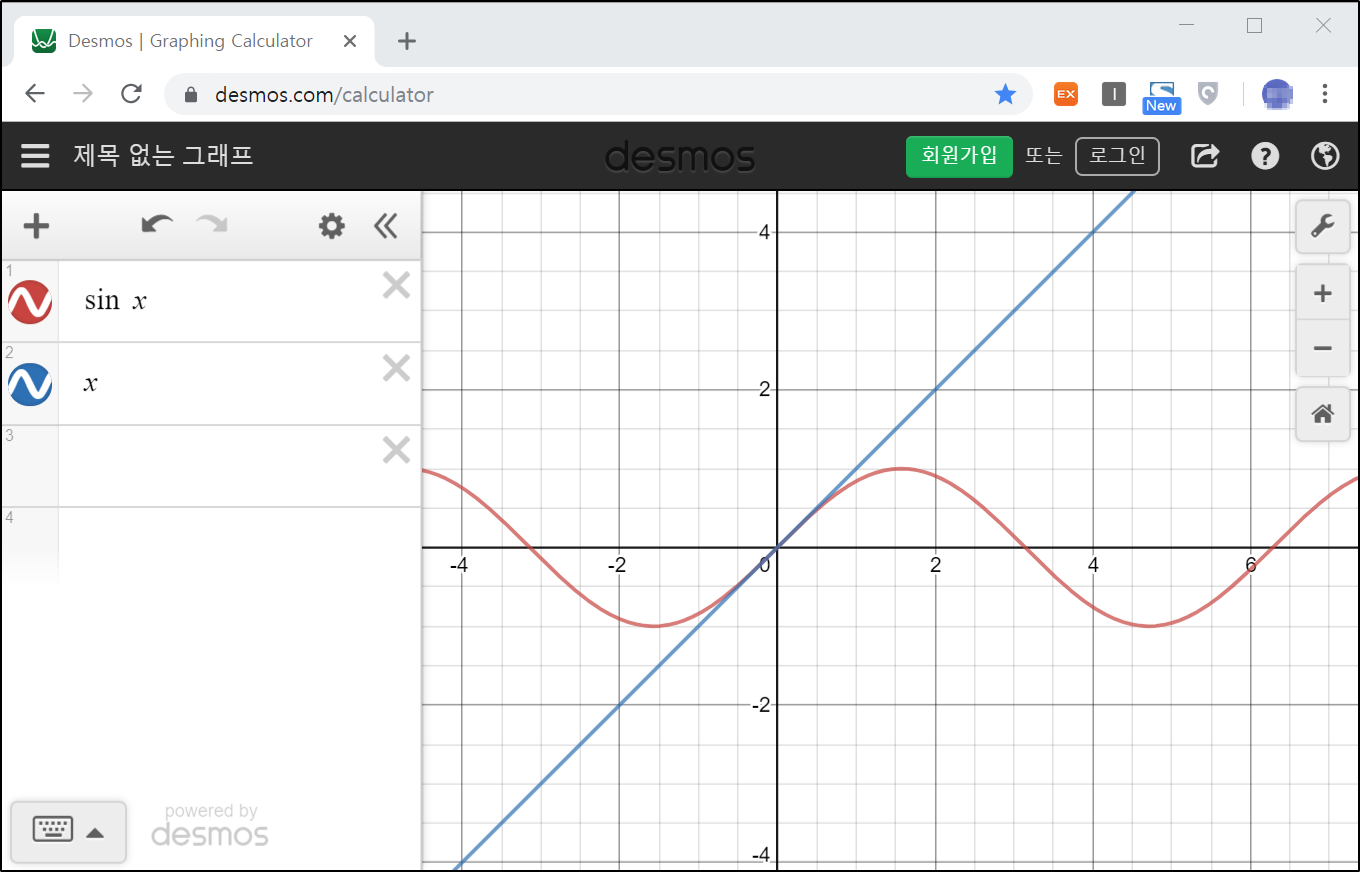
일단 y = x 그래프와 y = sin x 두개의 그래프를 그려보면 아래와 같다.
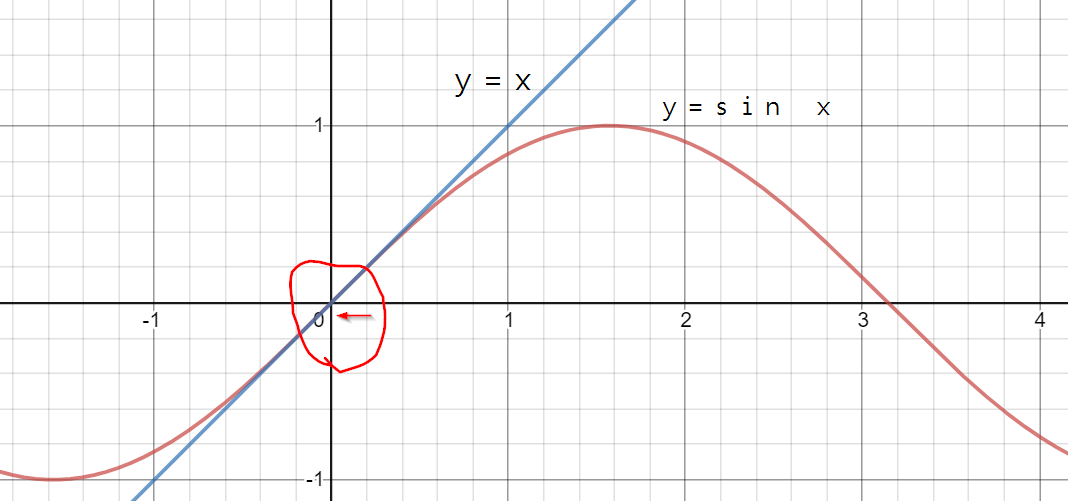
위에 빨간색 동그라미친 부분을 확대해 보았다. 음..
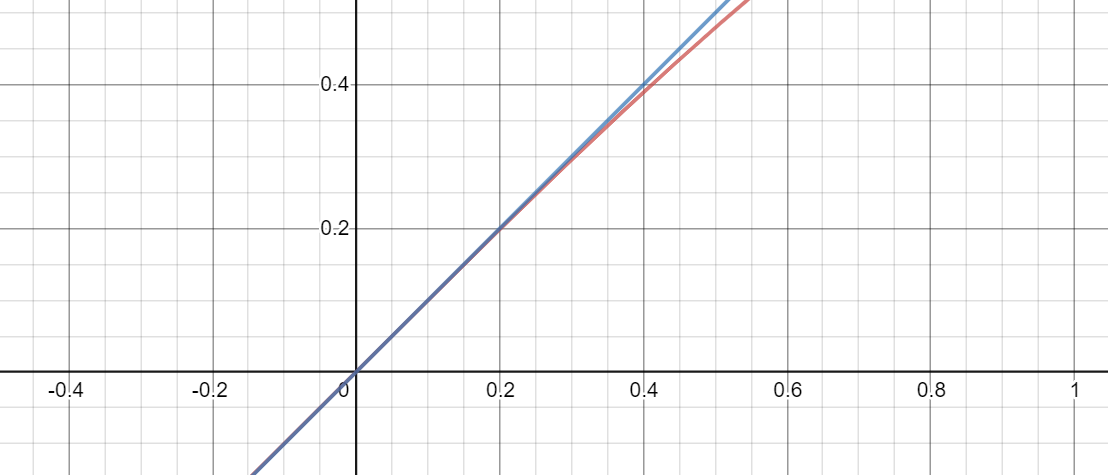
더 확대를 해보았다.
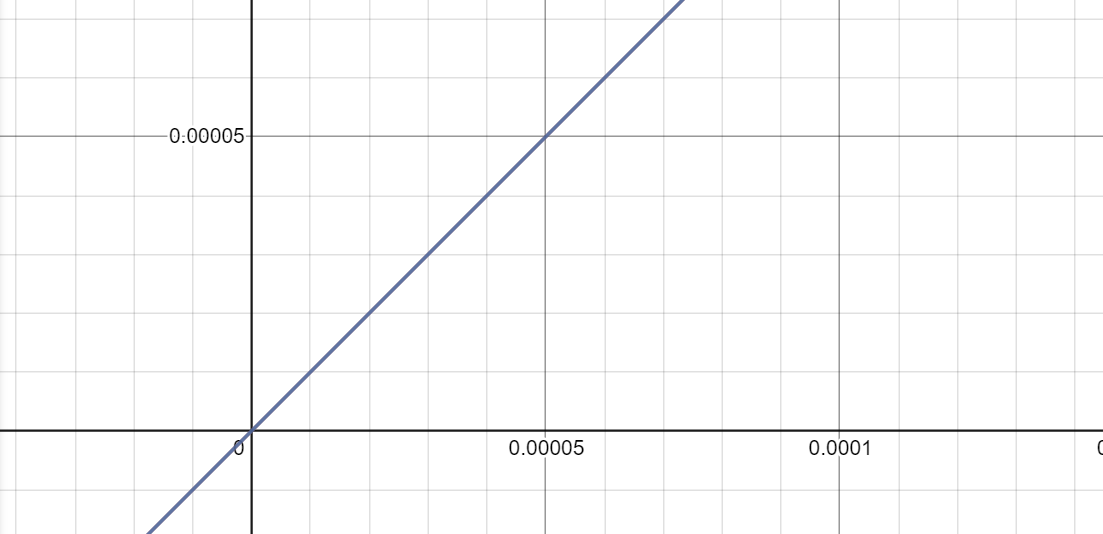
앗. 두개의 그래프가 거의 구분없이 붙어 버렸다.
이렇게 무한대로 계속 확대하다보면은 결국엔 1:1로 되어 극한값은 1이 되는 느낌..
그렇다면 두번째 실험 y = x 와 y = sin2x 는 어떤 느낌일까
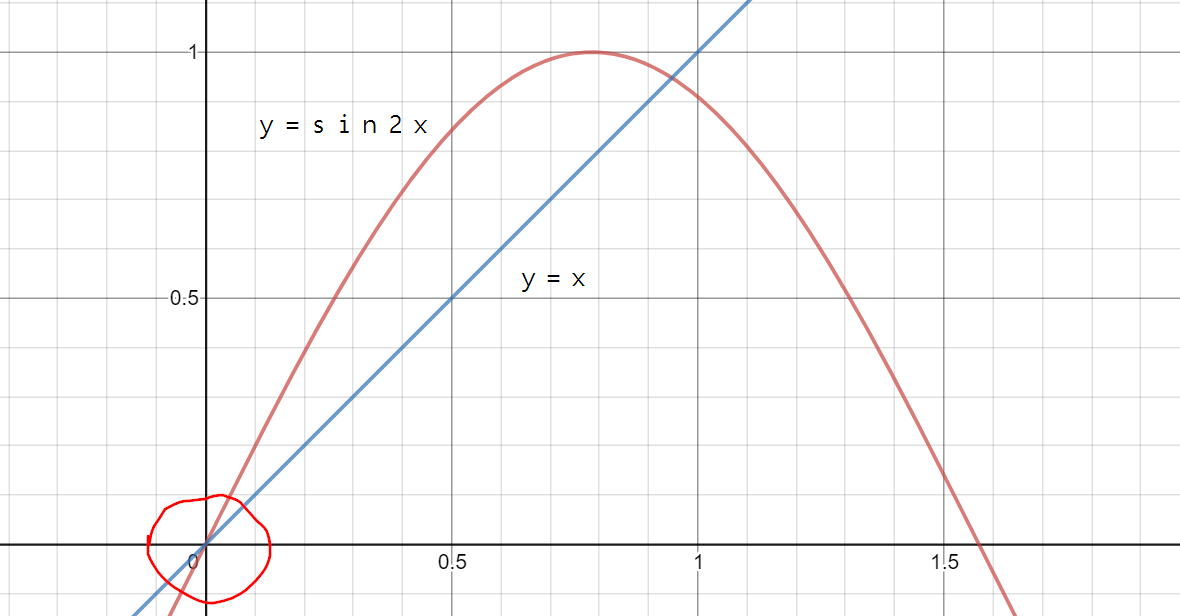
x값이 0으로 한없이 가까이 갈수록 y=sin2x 그래프가 y=x 그래프보다 더 빠른 속도로 0을 향해 변하고 있다.
y=sin2x 그래프가 변하는 속도는 2배일까?
좀 더 확대를 해보자
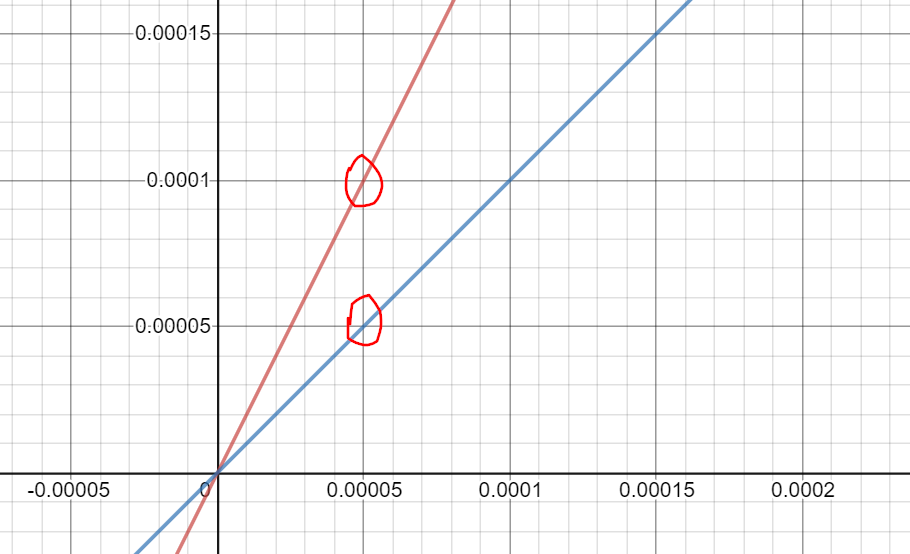
0으로 한없이 가까이 갈수록 y=sin2x 그래프가 y=x 그래프의 보다 2배인 느낌(!)
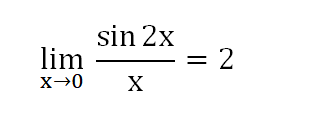
여기서 y=x 그래프를 y=2x로 바꾸면 두 그래프가 거의 일직선상으로 보인다.
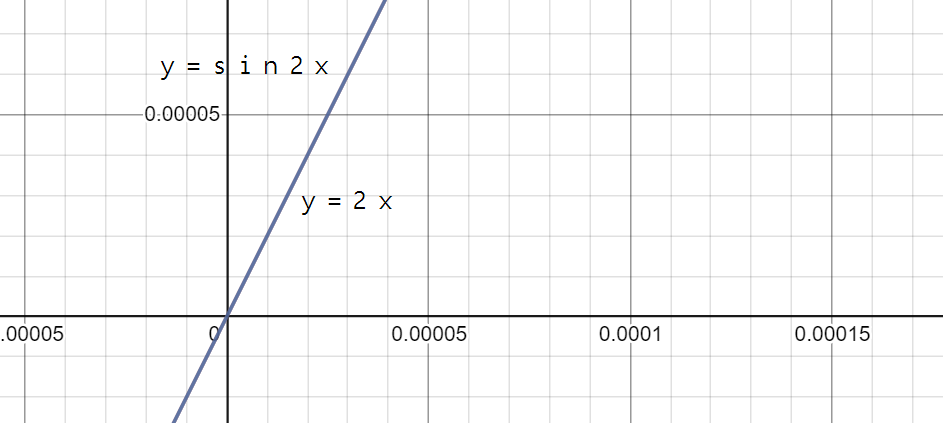
물론 현미경으로 들여다 보면 y=2x그래프가 미세하게 위에 있을것이다.
암튼 극한의 세계로 들어가게 되면 아래와 같게됨.
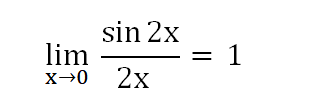
다시 정리를 해보면
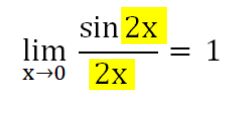
위에 노란색으로 칠해진 부분이 같다면 1로 수렴한다.
수학적인 증명은 아래 링크 참조
https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-8/v/sinx-over-x-as-x-approaches-0
참고로 그래프는 아래 사이트에서 생성하였습니다.
https://www.desmos.com/calculator
'AI > Math' 카테고리의 다른 글
| [미적분]미분공식 (0) | 2019.09.24 |
|---|---|
| [미적분]y=x^n 미분하기 (0) | 2019.09.24 |
| [미적분]몫의 미분법 (0) | 2019.09.24 |
| [미적분]y=a^x 지수함수 미분하기 (0) | 2019.09.23 |
| [미적분]Limit 너란 녀석 (0) | 2019.09.23 |